Fast Robots - Lab 11: Localization [real]
Bayes Filter [ simulation ]
In Lab 11, I implemented and tested grid-based localization on the real robot using a Bayes Filter. After verifying functionality in simulation, we deployed to hardware and collected real sensor data over BLE. The robot performed a full 360° rotation while logging yaw and distance (TOF) measurements, then used the Bayes Filter to infer its most probable location on a known map.
The simulation tests the Bayes Filter in a controlled environment. The red trajectory represents odometry-based motion prediction, the green line is ground truth, and the blue trajectory is the computed belief. The filter operates on a 3D grid (x, y, theta) and updates belief distributions at each step using odometry and sensor likelihood.
This part of the lab was unexpectedly time-consuming. I spent over 8 hours debugging environment mismatches, resolving dependency conflicts, and recreating virtual environments just to get the simulation running. Eventually, a clean reinstallation of Python and careful version management resolved the issues.
Bayes Filter [Real Robot]
The core functionality for the real robot was broken into two commands:
Artemis Code
This initiates the 360° rotation and sets up internal PID control for angular movement:
case ORIENTATION_CASE:
{
success = robot_cmd.get_next_value(run_ORIENTATION_CASE);
if (!success) return;
success = robot_cmd.get_next_value(setAngle);
if (!success) return;
success = robot_cmd.get_next_value(Kp);
if (!success) return;
success = robot_cmd.get_next_value(Ki);
if (!success) return;
success = robot_cmd.get_next_value(Kd);
if (!success) return;
if (run_ORIENTATION_CASE == 1) {
distanceSensor1.startRanging();
delay(3000);
// Reset state for collection
yawV = PyawV = total = 0;
count = end = 0;
start = 1;
b = i = h = 1;
stop = 360 / setAngle;
endTime = previousTime = millis();
}
Serial.print("run_ORIENTATION_CASE: ");
Serial.print(run_ORIENTATION_CASE);
Serial.print(" setAngle: ");
Serial.print(setAngle, 4);
Serial.print(" Kp: ");
Serial.print(Kp);
Serial.print(" Ki: ");
Serial.print(Ki);
Serial.print(" Kd: ");
Serial.println(Kd);
}
break;
This command is used after the orientation routine completes, to send the yaw and distance data to the Python host:
case SEND_ORIENTATION_DATA:
{
Serial.print("Sending orientation data...");
for (int i = 0; i < 18; i++) {
tx_estring_value.clear();
tx_estring_value.append("T:");
tx_estring_value.append(timePID_O[i]);
tx_estring_value.append("|angle_arr:");
tx_estring_value.append(yaw_arr[i]);
tx_estring_value.append("|D1_mm:");
tx_estring_value.append(distance_data[i]);
tx_characteristic_string.writeValue(tx_estring_value.c_str());
}
}
break;
Python Code
This Python function collects the data transmitted over BLE and parses it into yaw and distance readings:
import numpy as np
import asyncio
def perform_observation_loop(self, rot_vel=120):
"""
Initiates a 360° rotation and collects 18 yaw/TOF readings from the real robot over BLE.
"""
# Initialize observation arrays
sensor_ranges = np.zeros((18, 1))
sensor_bearings = np.zeros((18, 1))
print("[INFO] Sending ORIENTATION_CASE command...")
self.ble.send_command(CMD.ORIENTATION_CASE, f"1|{rot_vel}|1|0|0") # run=1, setAngle=rot_vel, Kp=1, Ki=0, Kd=0
print("[INFO] Waiting for motion to complete...")
await asyncio.sleep(4.0) # adjust depending on real spin time
print("[INFO] Requesting data from robot...")
self.ble.send_command(CMD.SEND_ORIENTATION_DATA, "") # Triggers BLE data dump
data_lines = []
while len(data_lines) < 18:
if self.ble.has_data():
msg = self.ble.read_line().strip()
if msg.startswith("T:"):
data_lines.append(msg)
else:
await asyncio.sleep(0.01)
print("[INFO] Parsing robot data...")
for i, line in enumerate(data_lines):
try:
# Format: T:<time>|angle_arr:<yaw>|D1_mm:<distance>
parts = line.split("|")
yaw = float(parts[1].split(":")[1])
dist_mm = float(parts[2].split(":")[1])
dist_m = dist_mm / 1000.0
sensor_ranges[i] = dist_m
sensor_bearings[i] = yaw
except Exception as e:
print(f"[WARN] Skipped malformed line: {line}, Error: {e}")
self.obs_range_data = sensor_ranges
return sensor_ranges, sensor_bearings
The belief distribution is compared to the known ground truth location of the robot. The Bayes Filter output is visualized using cmdr.plot_gt() to mark true poses and compare them against the computed belief.
# cmdr.plot_gt(-0.9144,-0.6096) # -3,-2 = -0.9144, -0.6096
# cmdr.plot_gt(1.524,0.9914) # 5, 3 = 1.524, 0.9144
# cmdr.plot_gt(1.524,-0.9914) # 5, -3 = 1.524, -0.9144
cmdr.plot_gt(0,0.9914) # 0, 3 = 0, 0.9144
After testing, I plotted ground truth vs computed belief. Ground truth is green and comupted is blue.
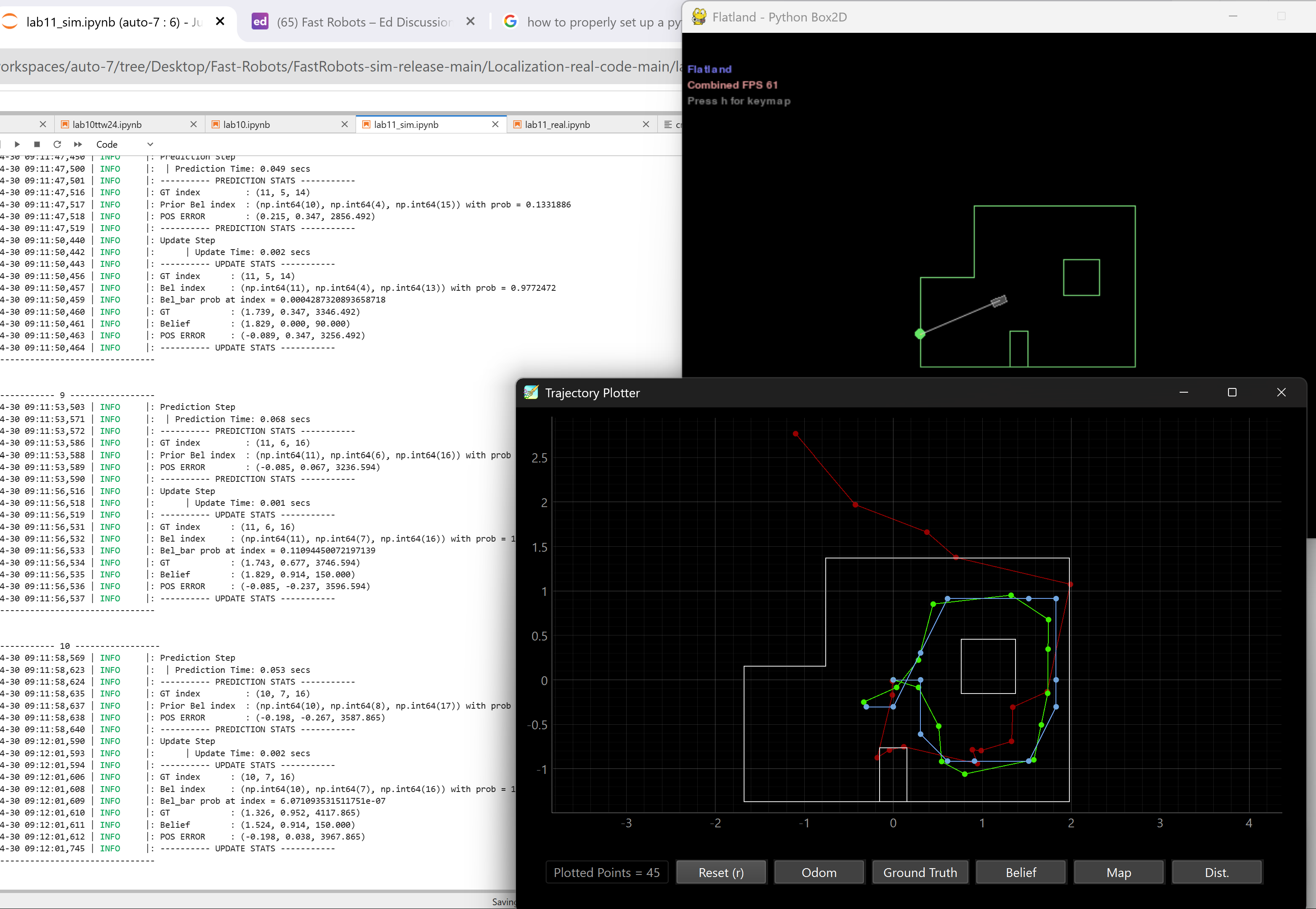
(-3,-2)
Ground truth pose: (-0.914, -0.914, 0.000)
Computed belief pose: (-0.914, -0.304, 60.0)
Resultant error: (0.000, 0.610, 60.0)
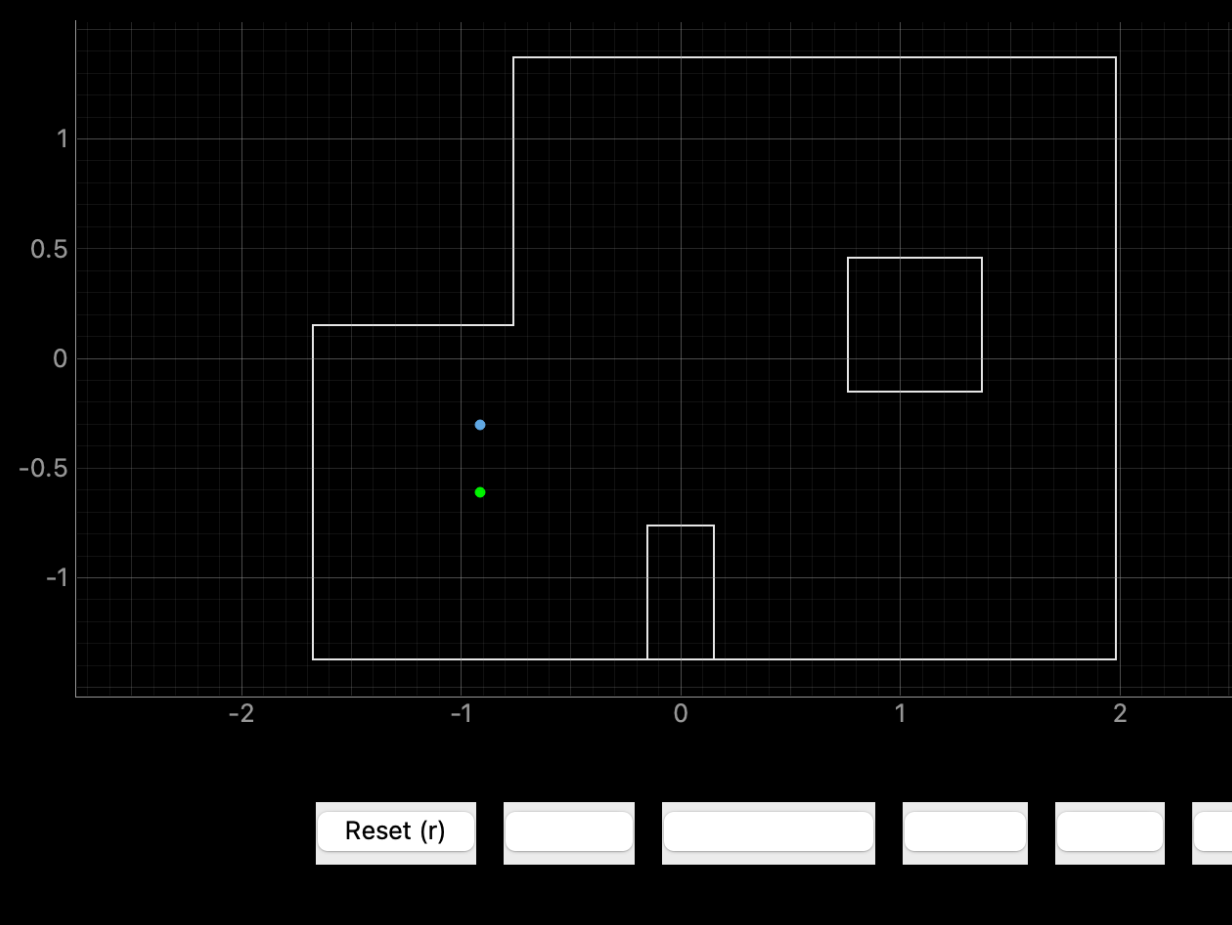
(5,3)
Ground truth pose: (1.524, 0.914, 0.000)
Computed belief pose: (1.821, 0.852, 70.0)
Resultant error: (0.297, 0.062, 70.0)
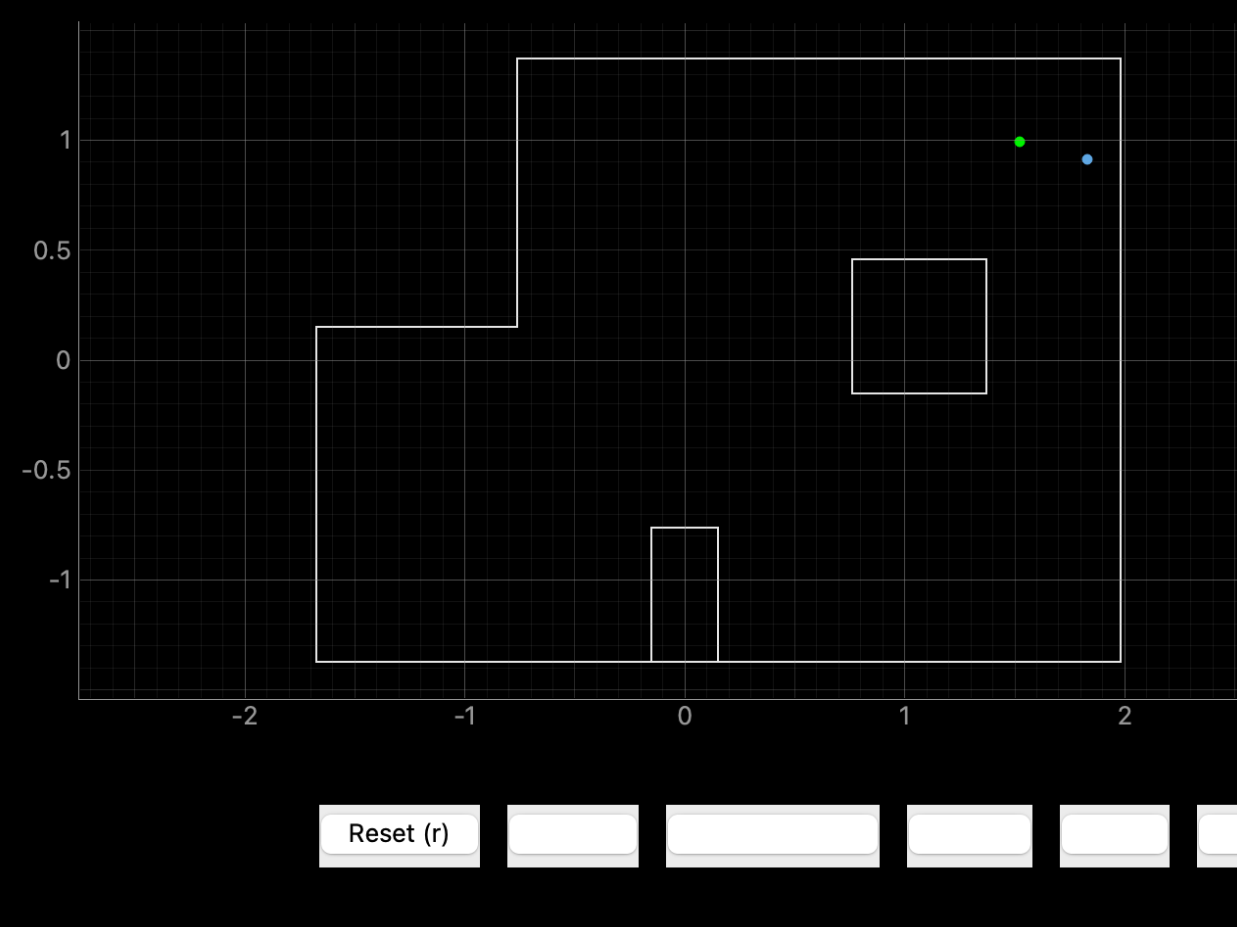
(5,-3)
Ground truth pose: (1.524, -0.914, 0.000)
Computed belief pose: (1.524, -1.054, 10.0)
Resultant error: (0.000, 0.140, 10.0 )
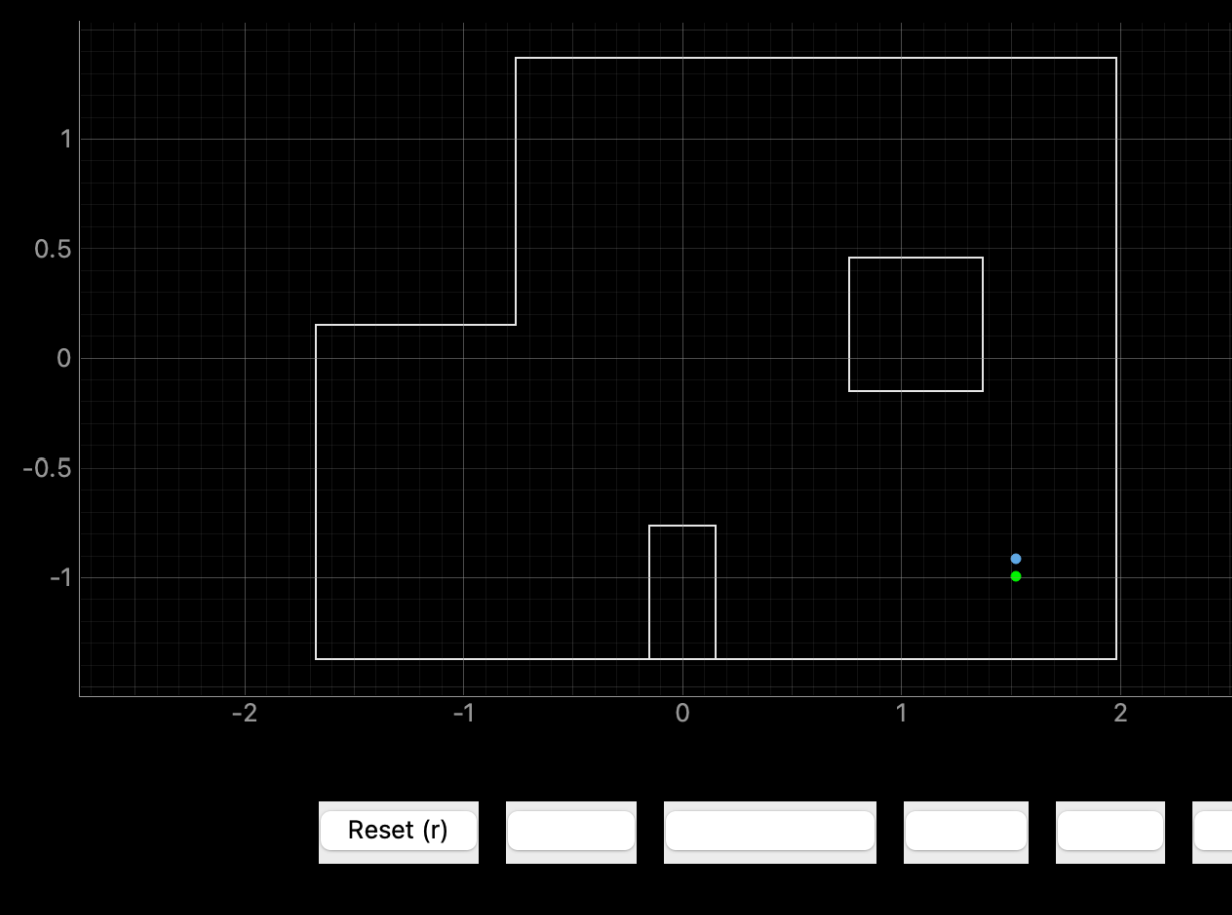
(0,3)
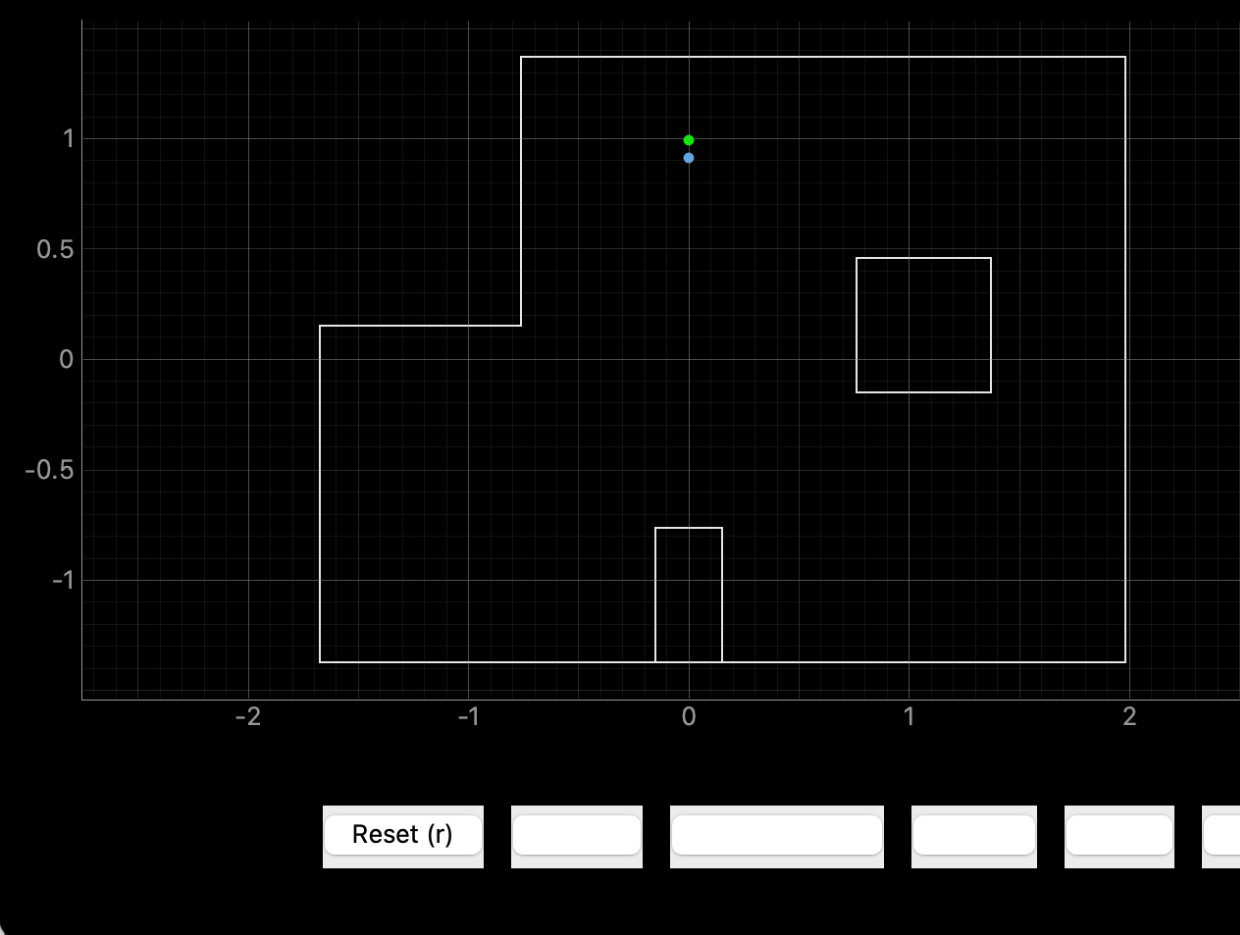
Ground truth pose: (0.000, 0.914, 0.000)
Computed belief pose: (0.000, 0.904, -10.0)
Resultant error: (0.000, 0.010, 10.0)
Conclusion
While not perfect, the Bayes Filter performed well under real-world noise. The largest errors occurred in orientation rather than position, which is expected given the limitations of single-sensor range-only localization with a fairly large (20 degree) swing between measurements. While not perfect, the Bayes Filter performed well under real-world noise. The largest errors occurred in orientation rather than position, which is expected given the limitations of single-sensor range-only localization with a fairly large (20 degree) swing between measurements.
